Tijdschrift voor Evidence-Based Medicine
Hazard Ratio versus Relatief Risico
Tekst onder de verantwoordelijkheid van de Nederlandstalige redactie
In dit nummer van Minerva bespreken we een open-label RCT (1,2) die het effect onderzocht van colchicine 0,5 mg per dag bij patiënten met stabiele coronaire hartziekte. Na een gemiddelde follow-up van 36 maanden werd bij 15 van de 282 (of 5,3%) patiënten in de colchicinegroep en bij 40 van de 250 (of 16%) patiënten in de placebogroep het primaire eindpunt (samengesteld uit acuut coronair syndroom, hartstilstand en CVA) geregistreerd. De verhouding van deze risico’s ((15/282)/(40/250)) levert een risk ratio of cohortonderzoek is dit relatieve risico een schatting van het aantal keren dat de kans om ziek te worden bij blootstelling aan een bepaalde risicofactor groter (RR>1) of kleiner (RR<1) is dan in de niet-blootgestelde groep. In een interventieonderzoek is dit relatieve risico een schatting van het aantal keren dat de kans op een uitkomst (bijvoorbeeld ‘genezing’) in de interventiegroep groter (RR>1) of kleiner (RR<1) is dan in de controlegroep. RR heeft geen dimensie. Bij het RR kan een 95%-betrouwbaarheidsinterval worden berekend.">relatief risico (RR) van 0,33 (95% BI van 0,18 tot 0,59) op. Dat betekent dus dat colchicine de kans op een cardiovasculaire gebeurtenis verlaagt met 67%.
De studie liep van begin september 2008 tot einde mei 2012. Door de inclusie van patiënten tot mei 2010 te laten doorlopen was het mogelijk om alle geïncludeerde patiënten minimum 24 en maximum 44 maanden op te volgen. Omwille van deze variatie in follow-up werden niet alle patiënten even lang behandeld en besloten de onderzoekers om hun resultaten uit te drukken in hazard ratio in de plaats van relatief risico.
Voor elke patiënt bepaalde men de ‘overlevingstijd’ of de tijd (in dagen) tussen enerzijds de dag van de randomisatie en anderzijds de dag waarop het primaire eindpunt zich voordeed ofwel de dag waarop de follow-up voor deze patiënt stopte zonder het primaire eindpunt te bereiken, omdat de studie stopte of omdat de patiënt vroegtijdig uit de studie viel. In het eerste geval, wanneer de patiënt door het eindpunt getroffen wordt, kunnen we een ‘exacte’ overlevingstijd berekenen (3). In het andere geval spreken we van een ‘gecensureerde’ overlevingstijd (4). Omdat er in de studie met colchicine tijdens de follow-up weinig patiënten getroffen werden door het eindpunt, waren er dus veel gecensureerde gegevens.
Op basis van deze individuele patiëntgegevens was het voor de auteurs vervolgens mogelijk om een Kaplan-Meier overlevingscurve te construeren (5,6).
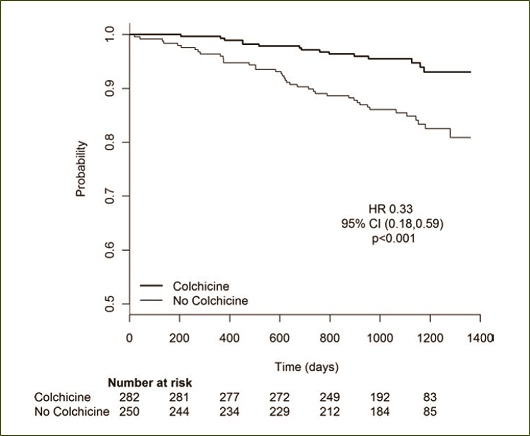
Op de X-as ziet men op elk moment van de follow-up hoeveel patiënten in elke groep de uitkomstmaat nog niet doormaakten (number at risk). De Y-as geeft voor elk moment van de follow-up voor elke groep de kans weer om niet door het eindpunt getroffen te worden.
Na 600 dagen zien we dat deze kans 0,98 bedraagt in de colchicinegroep versus 0,93 in de controlegroep. Deze cijfers komen overeen met een risico van respectievelijk 0,02 en 0,07 om door het primaire eindpunt wel getroffen te worden. De verhouding van deze risico’s leidt dan tot een risk ratio of relatief risico van 0,28 voor 501 patiënten, die gedurende 600 dagen konden worden opgevolgd of m.a.w. de behandeling kregen. Na 1 200 dagen kunnen we een relatief risico van 0,35 berekenen. Voor deze vermindering in effectgrootte moeten we echter rekening houden met het feit dat het hier gaat om een subgroepanalyse met slechts 83 patiënten in de colchicinegroep en 85 patiënten in de controlegroep die gedurende 1 200 dagen behandeld zijn.
Als clinicus zijn we echter vooral geïnteresseerd in het feit of er een significant en relevant verschil bestaat tussen de overlevingscurves van beide groepen en of dit verschil door de behandeling (colchicine versus geen colchicine) verklaard kan worden. Graag houden we hierbij ook rekening met de invloed van confounders (zoals hier: een verschil in gebruik van calciumantagonisten en bèta-blokkers). Met het Cox proportional hazards regression model (7) kan dan een hazard ratio berekend worden die het geschatte relatieve risico over de volledige studieduur uitdrukt en rekening houdt met deze confounders. Op deze manier kwamen de onderzoekers van de colchicinestudie tot een hazard ratio van 0,33 (95% BI van 0,18 tot 0,59). Deze hazard ratio komt hier dus perfect overeen met het hoger berekende relatieve risico. Dit betekent dat colchicine, onafhankelijk van de lengte van inname, de kans op het samengesteld eindpunt met 67% kans verlaagt. Dit was te verwachten omdat de overlevingscurves van bij het begin gelijkmatig divergeerden en de relatieve risico’s dus weinig verschilden in de tijd (5,7). Bij studies waarbij deze divergentie niet gelijkmatig verloopt, is de hazard ratio niet betrouwbaar en moeten we de overlevingscurves analyseren om het effect van de behandeling in functie van de tijd te beoordelen. Bij studies waarbij de overlevingscurves elkaar kruisen is het bovendien niet correct om een hazard ratio te berekenen.
Besluit
In vergelijking met een relatief risico houdt een hazard ratio rekening met de duur van een interventie. Ze geeft een verschil weer in aantal gebeurtenissen tussen de interventie- en de controlegroep die zich tijdens het verloop van de studie voordoen en houdt rekening met eventuele confounders. Een hazard ratio is alleen betrouwbaar wanneer de overlevingscurves gelijkmatig divergeren in de tijd.
- Christiaens T. Lage dosis colchicine voor secundaire preventie van cardiovasculaire ziekte? Minerva 2013;12(10):119-20.
- Nidorf SM, Eikelboom JW, Budgeon CA. Low-dose colchicine for secondary prevention of cardiovascular disease. J Am Coll Cardiol 2013;61:404-10.
- Sedgwick P. Hazards and Hazard ratio. BMJ 2012;345:e5980.
- Sedgwick P. Survival (time to event) data: censored observations. BMJ 2011;343:d4816.
- Petrie A, Sabin C. Medical Statistics at a glance. 3rd edition. Wiley-Blackwell 2009.
- Spruance SL, Reid JE, Grace M, Samore M. Hazard ratio in clinical trials. Antimicrob Agents Chemother 2004;48:2787-92.
- Sedgwick P. Cox proportional hazards regression. BMJ 2013;347:f4919.
Auteurs
Poelman T.
Vakgroep Volksgezondheid en Eerstelijnszorg, UGent
COI :
Trefwoorden
Cox proportional hazards model, hazard ratio, HR, Kaplan-Meier, methodologie, odds ratio, relatief risicoCodering
Commentaar
Commentaar